算法刷题前奏
前言
没事刷刷算法题,能够锻炼我们的逻辑思维,在日常编码中也会不由自主的关注编写程序的性能,还能防老年痴呆。
做算法题前,先了解一些常见的数据结构、算法及其时间复杂度。
时间复杂度
时间复杂度,一般分为最好情况、最快情况、平均情况、均摊。
分析方式:
加法法则:总复杂度等于量级最大的那段代码的复杂度。
乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积。
复杂度量级:
常数阶:O(1)
对数阶:O(logn)
线性阶:O(n)
线性对数阶:O(n logn)
平方阶:O(n2)、O(n3)、…
指数阶:O(2^n)
阶乘阶:O(n!)
常见数据结构
数组
概念:一种线性表数据结构;用一组连续的内存空间存储类型相同的一组数据。
特点:
随机访问快;插入删除慢。
链表
概念:通过“指针”将不连续的内存区域串联起来。
特点:查找慢;插入速度快,只需改变相邻节点的指针。
有单链表、双向链表、循环链表。
栈
概念:一种特殊的线性表,只能在一端进和出。
特点:先进后出。
用数组实现的栈叫顺序栈,用链表实现的栈叫链式栈。
队列
概念:一种操作受限的线性表结构。
特点:先进先出。
有顺序队列、链式队列、循环队列、阻塞队列、并发队列。
散列表
概念:通过散列函数将元素的键值映射成下标,并将数据存储在数组对应下标的位置。属于数组的一种扩展。
特点:需要有散列函数;装载因子,散列表的装载因子等于填入表中的元素个数/散列表的长度。
如果遇见散列函数执行后,多个键冲突(键不相等),可以使用开放寻址法(冲突后重新探测)或链表法。
二叉树
概念:每个节点最多有两个子节点,分别为左、右节点。
节点高度:节点到叶子节点的最长路径(边数)
节点深度:根节点到该节点的所经历的边的个数
节点层数:节点深度+1
树的高度:根节点的高度。
分类:
满二叉树:叶子节点都在最后一层。
完全二叉树:叶子节点都在最后两层,且最后一层的叶子节点都靠左排列。
堆
概念:首先是一个完全二叉树,其次每一个节点的值都必须小于等于或大于等于其子树中每个节点的值。
Trie树
概念:也叫字典树,一个树形结构。
例如以下字符串:b,abc,abd,bcd,abcd,efg,hii
构造后的树:
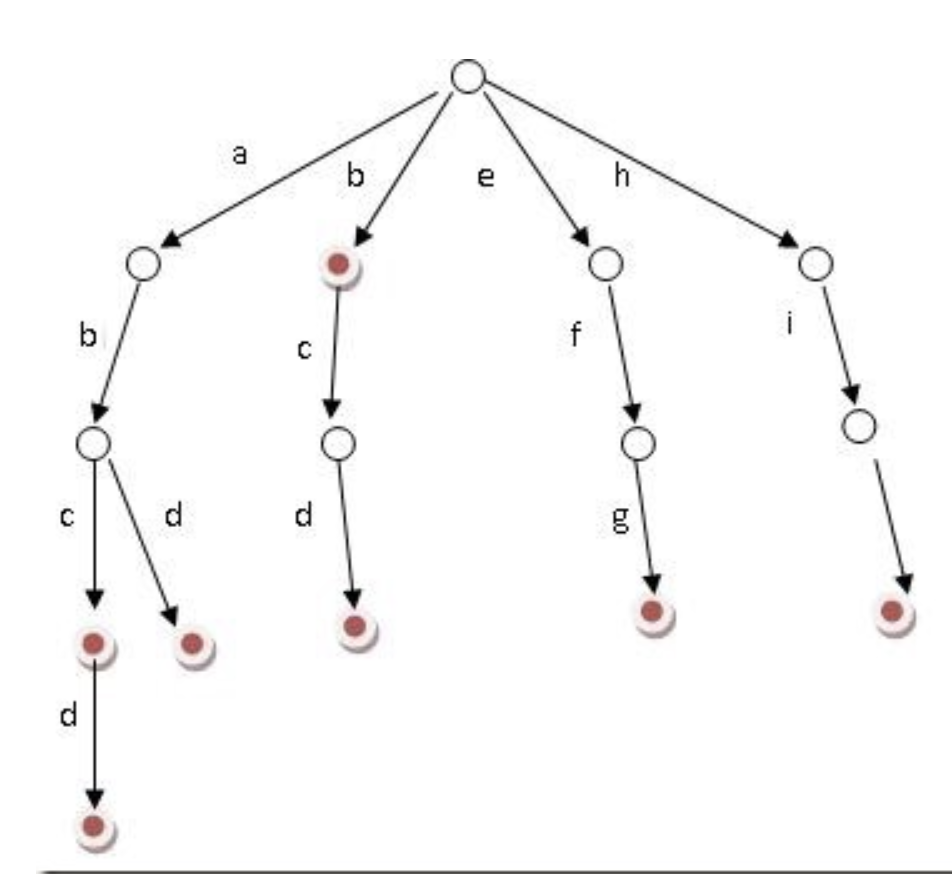
特点:利用公共前缀来提高字符串的查找速度。
图
概念:一种非线性数据结构。
分类:有向图、无向图、带权图
跳表
概念:一种单链表加多级索引的方式,可以加快检索,以空间换时间。
特点:相对于单链表,查询速度更快。
常见算法与模板
树节点定义
class TreeNode{
int val;
private TreeNode left;
private TreeNode right;
private List<TreeNode> getChildren() {
return Collections.emptyList();
}
public TreeNode(){}
public TreeNode(int val){
this.val = val;
}
}
广度优先遍历模板
/**
* BFS:广度优先遍历
* 除了遍历树,还可以遍历图
*/
public void BFS(TreeNode t, TreeNode start, TreeNode end) {
Queue<TreeNode> queue = new LinkedList();
queue.add(start);
// 遍历队列
while(!queue.isEmpty()) {
// 获取节点
TreeNode node = queue.poll();
// 处理节点
// process(node);
// 找当前节点的所有子节点
List<TreeNode> nodes = null;
// nodes = generate_related_node(node);
queue.addAll(nodes);
}
// other processing work
}
深度优先遍历模板
/**
* DFS:深度优先遍历
* 除了遍历树,还可以遍历图
* @Param t:当前遍历的节点
* @Param visited:是否已遍历,全局变量
*/
public void DFS(TreeNode t, Set<TreeNode> visited) {
visited.add(t);
// process current node here...
for (TreeNode child : t.getChildren()) {
if (!visited.contains(child)) {
// 递归访问
DFS(child, visited);
}
}
}
递归模板
/**
* 递归模板
* @Param level:层级,也可能是递减序列等
* @Param params:参数
*/
public void recursion(int level, Object params) {
// 1、recursion terminator(important)
if (level > MAX_LEVEL) {
// print_result
return;
}
// 2、process logic in current level
// process_data(level, data...)
// 3、drill down
recersion(level + 1, params);
// 4、may be reverse the current level status if needed
// reverse_status(level);
}
二分查找模板
/**
* 二分查找算法模板
* @Param array:数组
* @Param target:目标数据
*/
public void halfSearch(int[] array, int target) {
int left = 0;
int right = array.length - 1;
while(left <= right) {
int mid = left + (right - left) / 2;
if (array(mid) == target) {
// find target
return;
} else if (array[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
动态规划模板
/**
* 动态规划
*/
public int dp(int n, int m) {
// 1、状态的定义(重要)
// 可能是1维、2维、3维
int[][] dp = new int[n+1][m+1];
// 初始化状态
dp[0][0] = 0;
dp[0][1] = 0;
// 可能还有其它的
// 3、dp状态的推导(状态方程,重要)
for (int i = 0; i <=n; i++ ) {
for (int j = 0; j <= m; j++) {
// 动态方程表现...(如下示例)
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]);
}
}
// 返回最优解
return dp[n][m];
}
一些思路和技巧
1、递归 + 记忆法 =》递推
如计算斐波那契数列
2、位运算操作
1)、X & 1== 1 OR == 0 =》判断奇偶( X % 2 == 1),不管x是正还是负数
2)、X = X & (X - 1) =》清零最低位的1,不管x是正还是负数
3)、X & -X =》得到最低位的1,不管x是正还是负数
3、DP vs 回溯 vs 贪心
回溯(递归):重复计算
贪心:永远局部最优
DP:记录局部最优子结构 / 多种记录值
4、链表的注意点
1)、理解指针或引用的含义
引用中存储的是变量的内存地址。 p.next = q 表示p节点的next指针存储了q节点的内存地址。
2)、警惕指针丢失和内存泄漏(C中)
反例:p节点后插入x,p.next = x; x.next = p.next;
3)、利用哨兵简化实现难度
带哨兵节点的链表叫做带头链表
4)、重点留意边界条件处理
5)、举例画图,辅助思考
7)、多考虑使用双指针,特别是环之类的链表题目。
4、递归的3个条件和写法
1)、3个条件:问题可以拆解成子问题;子问题和原问题的解决思路一样;存在递归终止条件。
2)、写法:找规律写出递归公式,再找出终止条件,最后翻译成代码即可。
3)、递归可能的问题:堆栈溢出、重复计算、函数调用耗时高,空间复杂度高(堆栈)。
5、动态规划,满足一个模型3个特征
1)、一个模式:多阶段决策最优解模型(解决问题的过程,经过多个决策阶段,每个阶段有一个状态,寻找一组决策序列,最终获得最优解)
2)、3个特征:最优子结构、无后效性(只关注上一步,不用关注上上步;某阶段决策一旦确定,不受后面决策的影响)、重复子问题
一些资料
1、极客时间
王争《数据结构与算法之美》
谭超《算法面试通关40讲》
2、数据结构与算法可视化
(中文)http://www.rmboot.com/
(英文)https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
总结
只有坚持,才能慢慢熟能生巧。